How to set the padding of convolution to make the stride acting as a scale factor

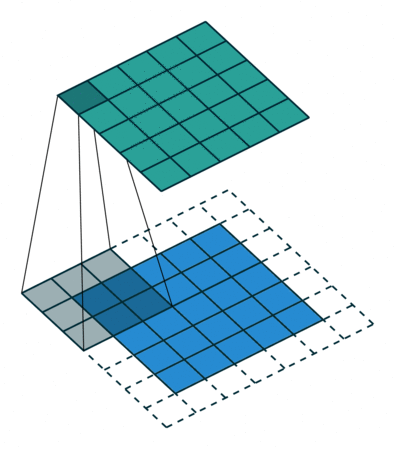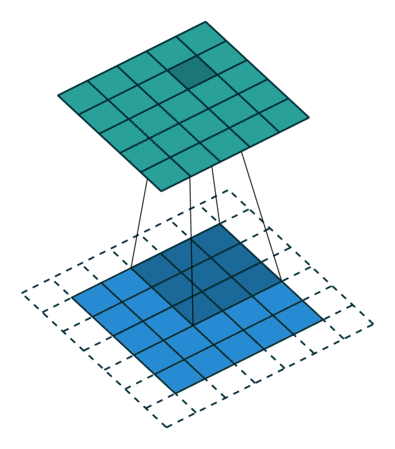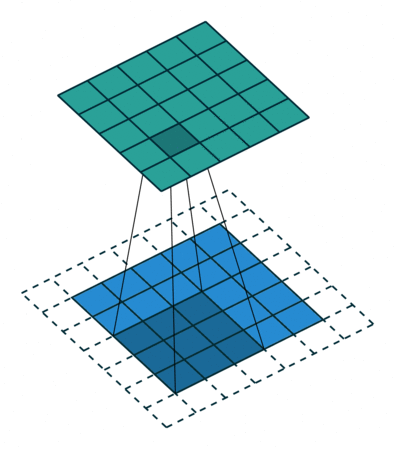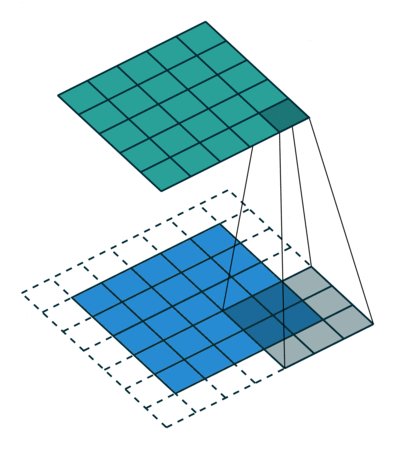
Cover image source: A guide to convolution arithmetic for deep learning - Vincent Dumoulin, Francesco Visin - ArXiv

When doing convolution, the kernel is shift around the input image. Let's consider the case when the kernel moves left-to-right. The up-to-down scenario are just the same.

Constrains

Let's denote the padding size as $p$, the image width as $w$, the kernel size as $k$, and the stride as $s$. Then the total length of image width plus padding should be:

$2p + w$

At the begging, the kernel is placed on the left of this total length, and is then moved towards right side with step length of $s$, until no more space is available. Denotes the number of the placable potions as $n$, then the output width of the convolution is also $n$. It should satisfys:

2p + w - s < k + (n-1) s \leq 2p + w \tag{a}

When will the stride $s$ acts as a scale factor? It can be formally written as:

n = \frac{w}{s} \tag{b}

Substitute (b) to (a) yields:

$2p + w - s < k + w - s \leq 2p + w$

The left side yields:

$p < \frac{1}{2}k$

And the right side yields:

$p \geq \frac{1}{2}(k - s)$

Thus:

$\frac{1}{2}(k - s) \leq p < \frac{1}{2}k$

When $k$ is even number

Since $p \in \mathbb{N}^{+}$, we must have

$s \geq 2$

Otherwise there would not be any available $p$. Then

$p = \frac{1}{2}k - 1$

P.S. Therefore, when $k$ is even number, size preserved convolution is not available.

When $k$ is odd number

Since $p \in \mathbb{N}^{+}$, then

$p = [\frac{1}{2}k]$
where $[\cdot]$ takes the integer part of the value.

This can be conveniently implemented as

p = k // 2