Clean Code Handbook: LeetCode 50 Common Interview Questions | LeetCode
Data structure
Array/string
- Transform & simplify combinatorial iterations
- Representation
- #13 Longest Palindromic Substring
Instead of representing the substring with starting and ending indices, represent it as center index and length is much more efficient, improving runtime from to .
- #13 Longest Palindromic Substring
- Proxy items
- #2 Two Sums II - Input Array Is Sorted
If the array is sorted, then . Thus can be used as a proxy of a bunch of other items in the iterations, improving the runtime to .
- #2 Two Sums II - Input Array Is Sorted
- Iteration folding
- #1 Two Sums
is commutative, thus half of the iteration steps can be saved and makes each iteration only previous items are relevant. Therefore, hash table of the previous items can be constructed in each iteration to accelerate later iterations, improving runtime from to . - #3 Two Sums III - Data Structure Design
- #6 Reverse Words in a String
Iterate from head to tail requires 2 passes, while from tail to head leads to a 1 pass algorithm.- #7 Reverse Words in a String II
By first reverse the whole strings, the order of words aligns with the desired output, thus the word-level reverse can be done in place. This further improves space complexity from to .
- #7 Reverse Words in a String II
- #1 Two Sums
- Problem split
- #10 Longest Substring Without Repeating Characters
When a string contains repeating characters, any substring of it is invalidated, thus the existence of repeating characters separates the combinatorial space into two subspaces. Considering that the longest possible substring can also be deduce from the location of the repeating characters, the runtime can be improved from brute force search to .
- #10 Longest Substring Without Repeating Characters
- Representation
- Marginal cases analysis
- #4 Valid Palindrome
- #5 Implement
strstr() - #8 String to Integer (
atoi) - #9 Valid Number
Parsing the digit structure with the optional components. - #12 Missing Ranges
- #14 One Edit Distance
- #15 Read N Characters Given Read4
Linked list
- Dummy head trick
Initialize a dummy head first can make your code simpler, since for the first and later iterations you're always adding new nodes to an existed node, avoiding conditional initialization logic embedded into the iteration loops. - #23 Merge K Sorted Linked Lists
Brute force merging can be implemented by merging 2 lists at a time sequentially, leading to runtime complexity. Divide and conquer mechanism can be used to improve the runtime down to . - #24 Copy List with Random Pointer
Deep copy a ordinary linked list is simple, whereas deep copy a linked list with an additional random pointer is tricky, since retrieve an item in the linked list costs runtime, leading to runtime complexity in total.
This can be improve to runtime and space by construct a hash map from the original items to the deep copied items.
The space complexity can be further improved to by first inserting the deep copied items after the original items, thus the hash map can be replaced withp.next. Then split deep copied ones from the original ones.
Binary tree
- Recursion
All nodes of a binary tree share similar structure, which makes recursion a particularly suitable choice for solving tree-related problems.
One thing to be noted is that recursion costs stack space, which should be considered when calculating the space complexity.- Information feedforward
- #25 Validate Binary Search Tree
Validate that any nodes are greater/less than all nodes of their left/right trees costs runtime with the brute force approach. With recursion, the max & min bound information can be feedforward down to each node for verification, improving runtime to .
- #25 Validate Binary Search Tree
- Information feedback
- #26 Maximum Depth of Binary Tree
Feedback the accumulative depth down from the leaf-nodes. - #28. Balanced Binary Tree
Feedback the accumulative depth down from the leaf-nodes and judge if the depths of the left and right trees differ no more than 1.
- #26 Maximum Depth of Binary Tree
- Divide-and-conquer
-
#31 Binary Tree Maximum Path Sum
Finding the maximum path sum seems to have giant combinatorial solution space, which makes even the brute force approach unimaginable - it's . Divide-and-conquer improves it to with the max path sum as the feedback information (feedbacks 0 when the current node is not included in the path).
- Information feedforward
- Depth-first traversal
Depth-first traversal of the binary search tree happens to be the ordered traversal of the nodes.-
#25 Validate Binary Search Tree
If the tree is a binary search tree, depth-first traversal provides a sorted list. Thus depth-first traversal can be used for verification in runtime. -
#30 Convert Sorted List to Balanced Binary Search Tree*
First acquire the length of the linked list, then the start, mid, end indices of the trees & subtrees can be depth-first traversed, which will happens to access the nodes from the linked list in order.
-
- Width-first traversal
Width-first traversal can be implemented with a queue: push the root to the queue. Then at each iteration, poll a node from the start of the queue and push all children to the queue.- #27 Minimum Depth of Binary Tree
Get the minimal depth when the first left node is reached in the width-first traversal.
- #27 Minimum Depth of Binary Tree
- Tree structure editing
This kind of problem is much more difficult than the others as it changes the tree structures at each step. Bear in mind that assigning a node as another node 's subtree doesn't delete 's links to its parent nor its subtrees. Be very careful!- #32 Binary Tree Upside Down
- Top-down approach: At each iteration, first keep copies of the current nodes left and right trees and then edit the current node: place the previous right node as the current node's left node and place previous edited node as the current node's right node - for accumulatively constructing an upside-down tree. Then set the kept left node as the current node and launch another iteration.
- Bottom-up approach: Constructing the bottom-up tree by recursion is way more intuitive, as shown in this figure:
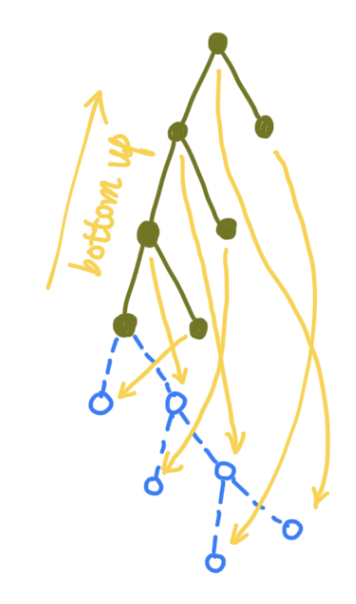
- #32 Binary Tree Upside Down
Stack
- #39 Min Stack
When we pop a stack, it's state will be changed. To access the state of the stack, e.g. its minimal item, we can record the stack state with another stack whenever we push it (or whenever we change its state). - Last-In-First-Out (LIFO)
In some problems, we only look for the adjacent elements to determine what to do next, e.g. parsing arithmetic notations and parentheses. In this case, the stack's LIFO property can be very useful.
Algorithm
Dynamic programming
The most important and challenging step of using dynamic programming is transforming the problem so that a dynamic programming formula can be formulated.
- #42 Climbing Stairs
Set as the number of ways you can climb to the -th step. Then - the Fibonacci sequence. - #43 Unique Paths
Set as the number of paths from cell to the bottom right cell. The . The calculation can be implemented with top-down recursion (from start cell) and ideally with memorization to improve its efficiency. But the bottom up implementation (from target cell) is way more efficient.- #44 Unique Paths II
Considering obstacle cells.
- #44 Unique Paths II
- #45 Maximum Sum Subarray
Set as the maximum sum of subarray ending at index . Let's assume 's subarray is . If , then is obviously .
However, if it's not true, is it possible to append a subarray of with to get the maximum sum of subarray ending at index ? Luckily, the answer is no. , thus any subarray of 's sum . Therefore, in this case, 's subarray should be itself.
In summary, .- #46 Maximum Product Subarray
The difficulty here is when is negative, could become the minimum subarray, while , the minimum subarray ending at index , becomes the maximum. Therefore, both are needed to be tracked and the dynamic programming formula is:
- #46 Maximum Product Subarray
- Memorization
- #47 Coins in a Line
The possible moves of you and your opponent are overwhelming. One critical idea is assuming that both you and your opponent will take the optimal move. Set as the maximum money one can take from the -th to the -th coins. When you are selecting between the -th and the -th coins, you minimize the maximum value your opponents could get from the remaining coins, and your opponents will do exactly the same. Therefore:
- #47 Coins in a Line
Binary search
Following is a basic template of binary search:
int L = 0, R = A.length - 1;
while (L < R) {
int M = (L + R) / 2;
// TODO: Implement conditional checks.
}
It's very subtle to avoid infinite loops: make sure either L or R must be updated in every loop! For example, when M is acquired via floor divide of (L + R)/2, then either L = M + 1 or R = M.
- #48 Search Insert Position
When target is within the range of the list's minimum/maximum, thenL/Rmust have been updated when the loop ends, whenL=R. Therefore,A[L-1] < targetandA[L+1] > targetand the insertion location can be easily deduced.
It's a little bit trick to understand the case when the target is less/greater than the minimum/maximum since in this caseL/Rcould keep unchanged and the size relationships don't hold. However, the insertion location should beLorL+1, exactly becauseLorRis never changed in this case. - #49 Find Minimum in Sorted Rotated Array
Misc
Math
- #17 Reverse Integer
Deal with overflow/underflow.
P.S. For 32-bitint, since 1 bit is used for storing the sign, the max/min value is . - #18 Plus One
Marginal case: 999. - #19 Palindrome Number
Digit parsing tricks.
Bit manipulation
- Tweaking commutative operation
When a commutative operation is applied to a chain of values, these values can be rearranged arbitrarily yet still get the same result. This property is particularly useful.- #33 Single Number
XOR detect changes between 2 bits. When XOR all of the numbers together, since XOR is commutative, we can group the repeating numbers together, which all become 0s. Therefore, the result will be the single number itself. ^ex-33 - #34 Single Number II
The same idea of #33 is used, but the commutative operation becomes: for each bit position, add all bits together and mod 3.
This can be implemented with a 32-lengthintarray. However, a more efficient approach uses 3 bitmasksones,twos, andthreesto represent the bits that appears to be on for 1, 2, and 3 times. The manipulation of these bitmasks requires some fascinating usage of logic operations.
- #33 Single Number

